leetcode刷题笔记-排列组合

用于记录leetcode刷题中遇到的排序与组合问题的解法

首先给出排列组合问题的定义，排列组合是组合学最基本的概念。所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排列。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑这些元素间的排列顺序

目前在leetcode中，排列组合题目的难点是对于重复元素的处理，接下来进行详细的总结

组合问题

不包含重复数字的组合问题

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。详见 77. 组合

一般采用 递归+回溯 的方法，标准模板如下：

vector<int> temp;
void dfs(int cur, int n) {
    // 记录合法的答案
    if (temp.size() == k) {
        ans.push_back(temp);
        return;
    }
    // cur == n + 1 的时候结束递归
    if (cur == n + 1) {
        return;
    }
    // 考虑选择当前位置
    temp.push_back(cur);
    dfs(cur + 1, n, k);
    temp.pop_back();
    // 考虑不选择当前位置
    dfs(cur + 1, n, k);
}

不包含重复数字的组合问题，同时限制组合数的和

找出所有相加之和为 n 的 k个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

• 所有数字都是正整数。
• 解集不能包含重复的组合。 详见216. 组合总和 III

包含重复数字的组合问题

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中包含有重复的数字，但是其中每个数字在每个组合中只能使用一次。详见 40.组合总和 II

难点在于：

备选序列包含有重复的数字，但是最后的答案中不能含有相同的组合序列

举个例子：

wiki

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

由于含有两个1，因此按照之前的方法，我们可能在最终答案中包含[1, 7]，[7, 1]两个组合序列， 这个是不符合题目要求的。

我们的改进方法是：将相同的数放在一起进行处理，也就是说，如果数 x 出现了 y 次，那么在递归时一次性地处理它们，即分别调用选择 0, 1,⋯ y 次 x 的递归函数。这样我们就不会得到重复的组合。

具体做法是：对于序列[10,1,2,7,6,1,5]，我们先统计每个元素出现的次数，即：{1:2，2:1，5:1，6:1，7:1，10:1}；在进行 递归+回溯 时，我们需要处理的序列是[1, 2, 5, 6, 7, 10]，此时已经不再包含重复的元素

排序问题

不包含重复数字的排序问题

此时问题与不包含重复数字的组合问题完全相同

包含有限个重复数字的排序问题

有重复字符串的排列组合。编写一种方法，计算某字符串的所有排列组合。详见 面试题 08.08. 有重复字符串的排列组合

举个例子：

wiki

输入：S = "qqe"
输出：["eqq","qeq","qqe"]

难点在于：

给定的字符串中存在重复的字符，在进行排列时，需要将重复的字符去除。具体如下图所示：

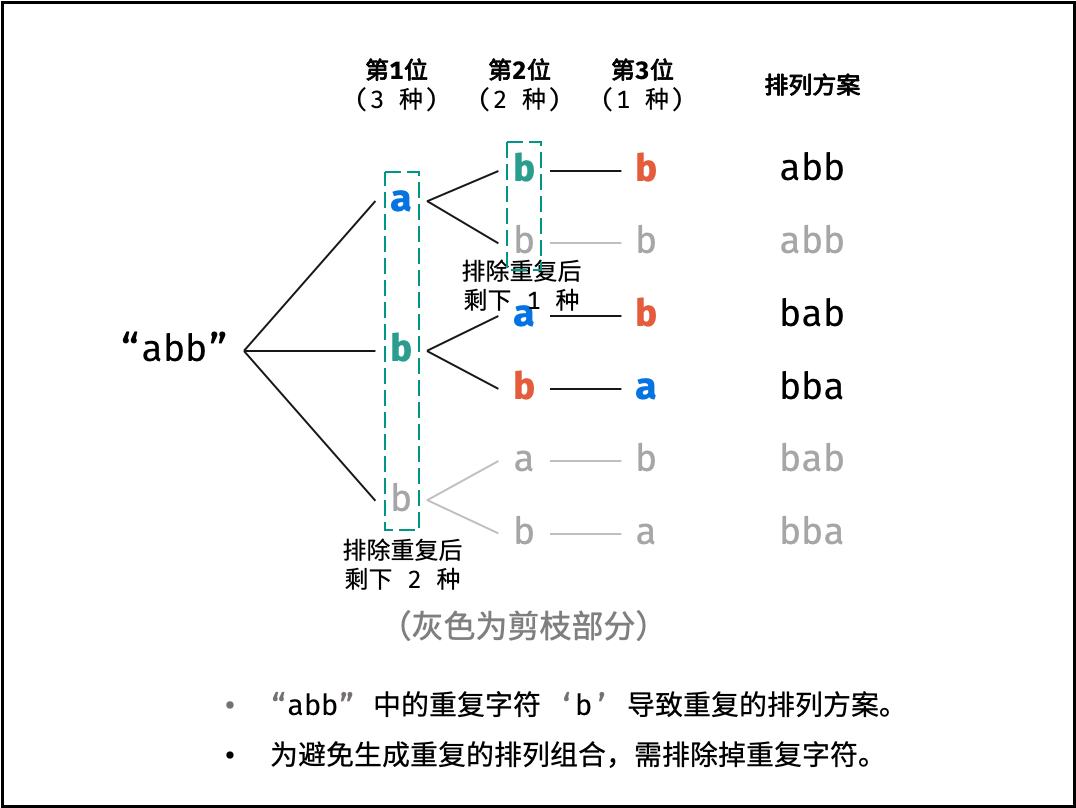
为了实现在图中的每一位排除重复出现的字符，我们使用了set，具体代码如下所示：

class Solution:
    def permutation(self, s: str) -> List[str]:
        n = len(s)
        visited = [0]*n
        res = []
        def dfs( tmp, visited, s):
            if len(tmp)==n:
                res.append(tmp)
                return
            hashset = set()
            for i in range(n):
                if s[i] not in hashset and visited[i]==0:
                    hashset.add(s[i])
                    visited[i] = 1
                    dfs(tmp+s[i], visited, s)
                    visited[i] = 0
        dfs("", visited, s)
        return res

包含无限个重复数字的排序问题

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。详见 377. 组合总和 Ⅳ

举个例子：

wiki

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的排列为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同。

解法：

此题适合使用动态规划，即：

• 初始化 dp[0]=1；
• 遍历 i 从 1 到 target，对于每个 i，进行如下操作：
  • 遍历数组 nums 中的每个元素 num，当 num≤i 时，将 dp[i−num] 的值加到 dp[i]。
• 最终得到 dp[target] 的值即为答案。