(SVM)支持向量机算法
SVM用于解决二分类问题
在数学中,超平面是n维空间中的n-1维的子空间。它是平面中的直线、空间中的平面之推广。
SVM的学习策略:间隔最大化
支持向量机的机制就是在多种正确的分类器中挑选泛化能力最强的分类器
SVM基础的工作原理。下面是SVM的基础特性:
找到对训练集所有的正确划分(超平面)
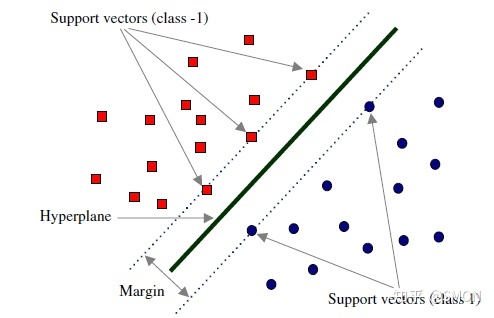
在所有正确的划分中选择距离最近数据点距离最大的那个决策边界,即被尽可能宽的间隔明显的分隔开
线性可分SVM
当训练数据线性可分时,通过硬间隔(hard margin)最大化可以学习得到一个线性分类器,即硬间隔SVM
回忆一下感知机的目标: 找到一个超平面使其能正确地将每个样本正确分类。感知机使用误分类最小的方法求得超平面,不过此时解有无穷多个(例如图1.1的H2和H3以及它俩的任意线性组合)。而线性可分支持向量机利用间隔最大化求最优分离超平面,这时解是唯一的。
在线性可分的情况下,训练数据集的样本点中与分离超平面距离最近的数据点称为支持向量
线性SVM
当训练数据不能线性可分但是可以近似线性可分时,通过软间隔(soft margin)最大化也可以学习到一个线性分类器,即软间隔SVM。即可以带有一定的容错率,但是对错误分类的样本会有惩罚,惩罚参数为C
线性不可分SVM
将非线性可分的数据映射到一个线性可分的空间(高维空间),然后在这个空间找超平面。即通过使用核技巧(起到映射作用)(kernel trick)和软间隔最大化,可以学习到一个非线性SVM。
参考资料
[1] 深入浅出SVM
(SVM)支持向量机算法