决策树算法
之前介绍的k-近邻算法可以完成很多分类任务,但是它最大的缺点就是无法给出数据的内 在含义,决策树的主要优势就在于数据形式非常容易理解。
决策树的一个重要 任务是为了数据中所蕴含的知识信息,因此决策树可以使用不熟悉的数据集合,并从中提取出一系列规则,在这些机器根据数据集创建规则时,就是机器学习的过程。
简单图示如下:
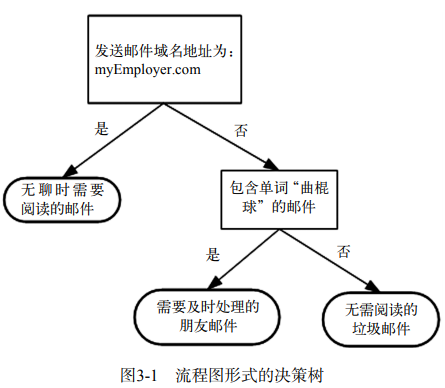
原理
其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。
使用决策树进行决策的过程就是从根节点开始,从所有属性中选取一个属性,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
接下来我们通过一个例子来展示决策树是如何应用在实际情况中的:
摘自参考资料[1]
假如我现在告诉你,我买了一个西瓜,它的特点是纹理是清晰,根蒂是硬挺的瓜,你来给我判断一下是好瓜还是坏瓜,恰好,你构建了一颗决策树,告诉他,没问题,我马上告诉你是好瓜,还是坏瓜?
判断步骤如下:
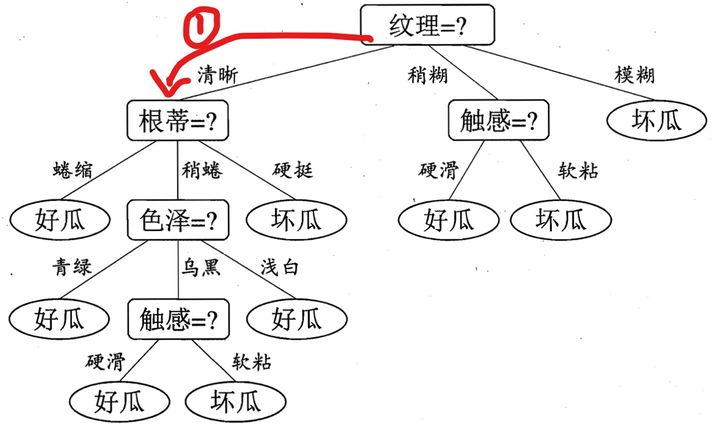
根据纹理特征,已知是清晰,那么走下面这条路,红色标记:
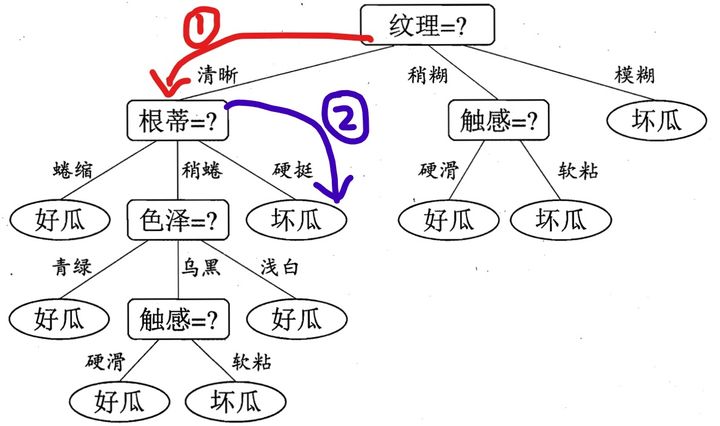
好的,现在咋们到了第二层了,这个时候,由决策树图,我们看到,我们需要知道根蒂的特征是什么了?很好,他也告诉我了,是硬挺,于是,我们继续走,如下面蓝色所示:
此时,我们到达叶子结点了,根据上面总结的点,可知,叶子结点代表一种类别,我们从如上决策树中,可以知道,这是一个坏瓜!
于是我们可以很牛的告诉他,你买的这个纹理清晰,根蒂硬挺的瓜是坏瓜,orz!
如何构建树
通过之前的决策树,我们可以看出来:每一次子结点的产生,是由于我在当前层数选择了不同的特征来作为我的分裂因素造成的。比如下图用红色三角形表示选择的特征
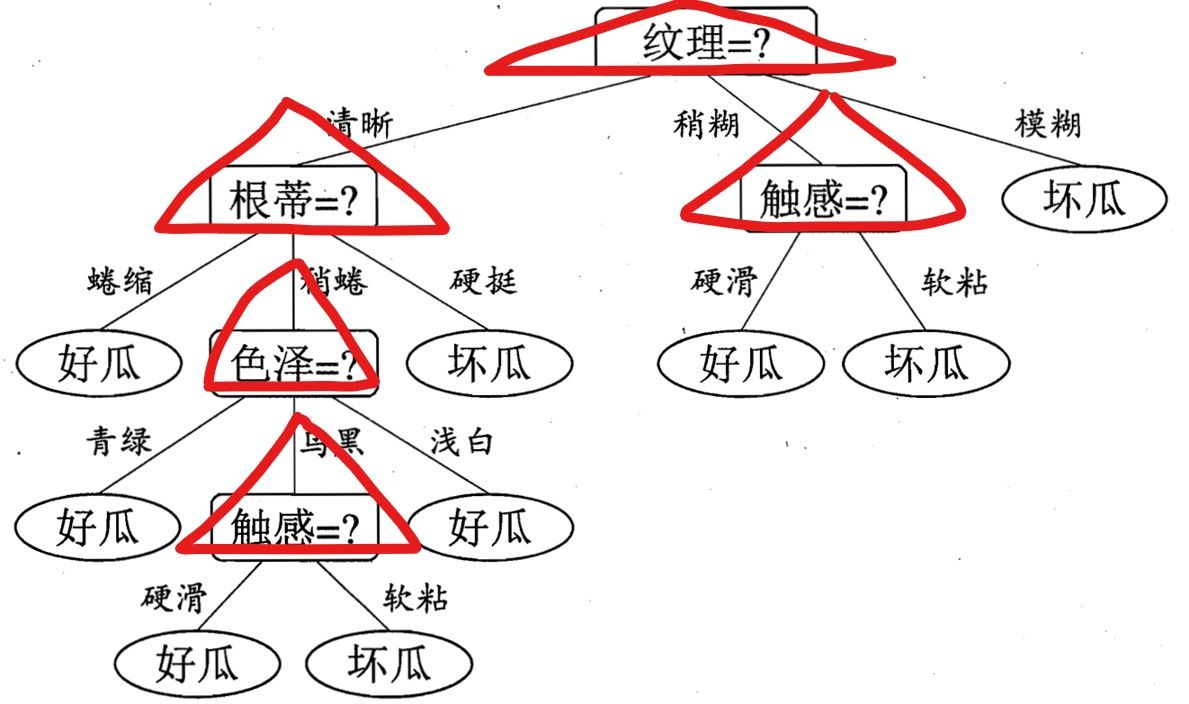
每一层选择了指定的特征之后,我们就可以继续由该特征的不同属性值进行划分,依次一直到叶子结点。
那么接下来的问题便是:在每一个分支节点,如何进行特征选择?
我们称分支节点为选择的属性为分裂属性,所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。
而判断“纯”的方法不同引出了我们的ID3算法,C4.5算法以及CART算法
特征选择
ID3算法
这里我们使用 信息增益 来作为集合纯度的衡量条件
信息熵是度量样本集合不确定度(纯度)的最常用的指标。
信息熵是代表随机变量的复杂度(不确定度),条件熵代表在某一个条件下,随机变量的复杂度(不确定度)。
我们对于信息增益的定义恰好是:信息熵-条件熵。
具体计算举例:
当前样本集合 D 中第 k 类样本所占的比例为 \(p_{k}\) ,则 D 的信息熵定义为: \[ \operatorname{Ent}(D)=-\sum_{k=1}^{|\mathcal{Y}|} p_{k} \log _{2} p_{k} \] 离散属性 a 有 V 个可能的取值 {a1,a2,…,aV};样本集合中,属性 a 上取值为 av 的样本集合,记为 Dv;则条件熵的定义为: \[ \sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(\begin{array}{l} \left.D^{v}\right) \end{array}\right. \] 因此最后我们得到信息增益如下: \[ {\text { Gain }}(D, a)=\operatorname{Ent}(D)-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right) \] 信息增益表示得知属性 a 的信息而使得样本集合不确定度减少的程度。
因此进行特征选择时,我们可以用信息增益来度量。如果选择一个特征后,信息增益最大(信息不确定性减少的程度最大),那么我们就选取这个特征。
C4.5算法
这里我们使用 信息增益率 来作为集合纯度的衡量条件