leetcode刷题笔记-并查集

并查集

并查集是一种 树形 的数据结构，它用于处理一些不交集的 合并 及 查询 问题。 它支持两种操作：

• 查找（Find）：确定某个元素处于哪个子集；
• 合并（Union）：将两个子集合并成一个集合。

物理结构属于树形结构，逻辑结构仍然是集合结构，即不关注树中的父子节点关系

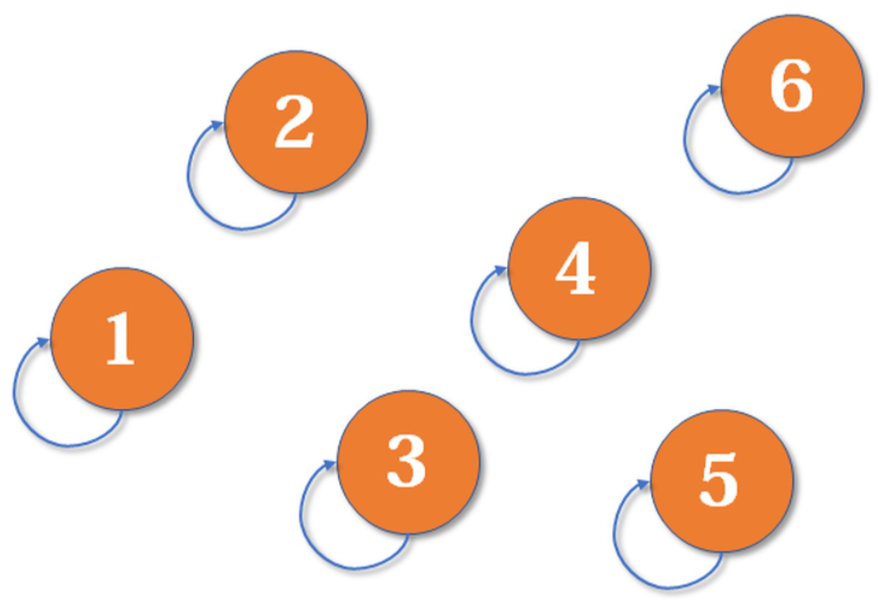
初始化

创建fa数组，表示当前节点的父节点，初始化时，每个节点指向自己

void makeSet(int size) {
    for (int i = 0; i < size; i++) fa[i] = i;  // i就在它本身的集合里
    return;
}

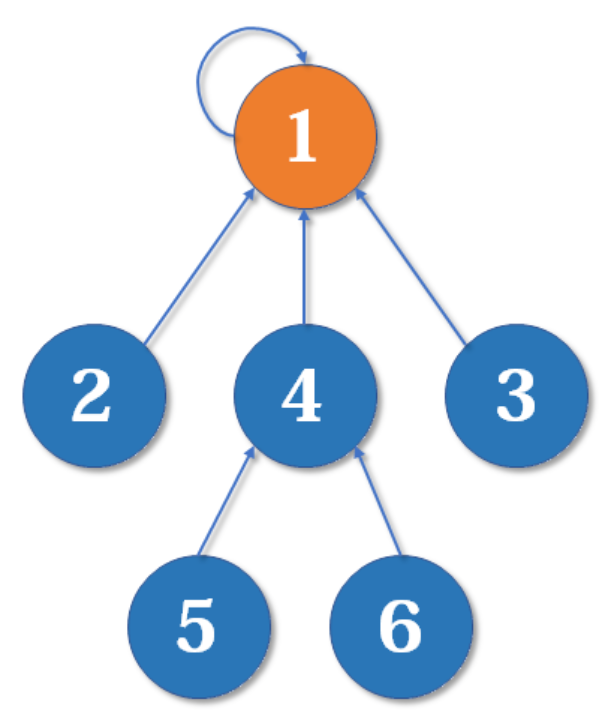
查找

我们将fa[x]==x的x视为一个集合的祖先，集合的祖先具有如下的特性：

1. 一个集合只有一个祖先，每个集合的祖先必不相同，可以作为当前集合的唯一标识
2. 当比较两个元素属不属于一个集合时，只用比较两个元素所在集合的祖先是否相同即可

未压缩

int find(int x) {
    // 寻找x的祖先
    if (fa[x] == x)  // 如果x是祖先则返回
        return x;
    else
        return find(fa[x]);  // 如果不是则x的爸爸问x的爷爷
}

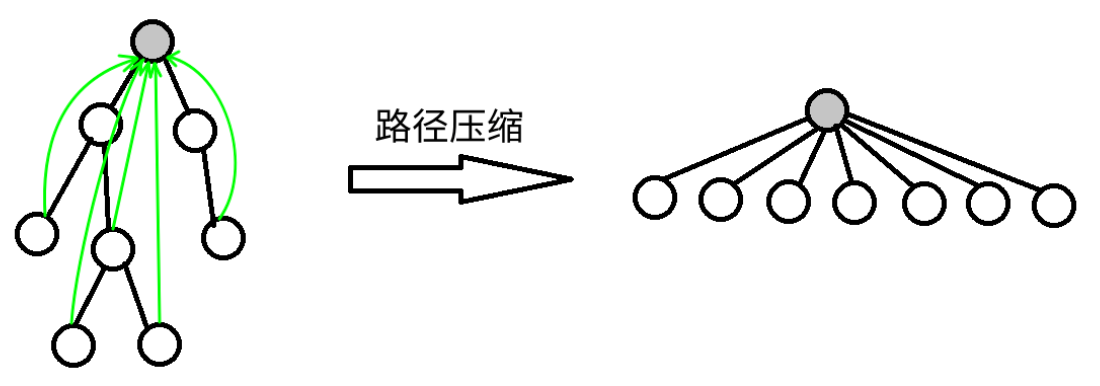
路径压缩

作用范围：find(x)会对x到祖先节点这条路径上的所有节点进行路径压缩，如下图所示，即为 find(x) 中加入路径压缩，在find(2)前后树状结构的变化

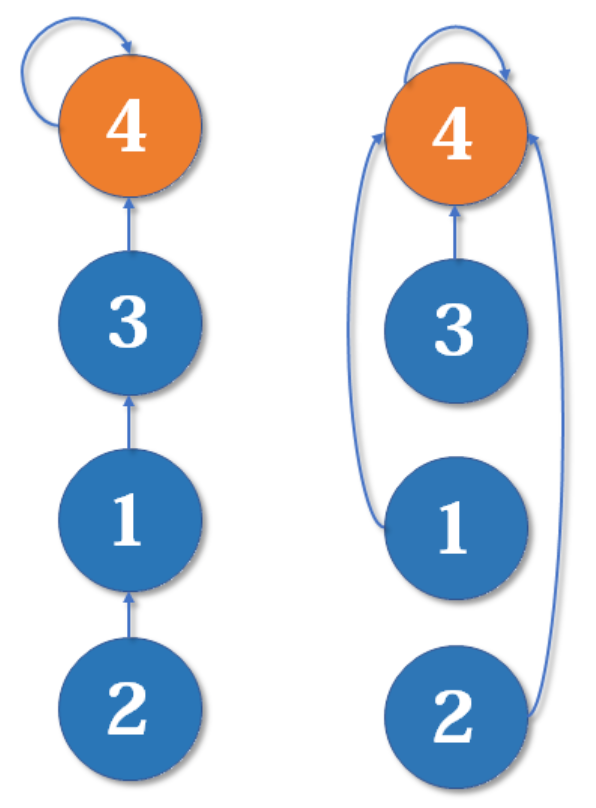
int find(int x) {
    if (x != fa[x])  // x不是自身的父亲，即x不是该集合的代表
        fa[x] = find(fa[x]);  // 查找x的祖先直到找到代表,于是顺手路径压缩
    return fa[x];
}

合并

合并两个元素所在的集合时，其本质就是让一个集合的祖先的fa[]指向另一个集合的祖先

void unionSet(int x, int y) {
  	// x 与 y 所在家族合并
  	x = find(x);
  	y = find(y);
  	fa[x] = y;  // 把 x 的祖先变成 y 的祖先的儿子
}

变体

按秩合并

如果我们将一棵点数与深度都较小的集合树连接到一棵更大的集合树下，显然相比于另一种连接方案，接下来执行查找操作的用时更小（也会带来更优的最坏时间复杂度）

带权并查集

在并查集的边上定义某种权值、以及这种权值在路径压缩时产生的运算，从而解决更多的问题

LeetCode题目：1631. 最小体力消耗路径

References

[1] 并查集

[2] 算法学习笔记(1) : 并查集