(KGIN)Learning Intents behind Interactions with Knowledge Graph for Recommendation 论文笔记

创新点
User Intents:将用户与商品之间的交互通过一个细粒度的角度考虑,即用户意图这个角度。一共存在n个用户意图向量,这些用户意图向量对于所有的用户都是相同的,从不同的角度决定了用户对于某一件商品的兴趣。最终决定用户对于一件商品的兴趣,即user vector——通过对于不同的intent vector赋予不同权重的加和。关于intent的图示化具体如下所示:
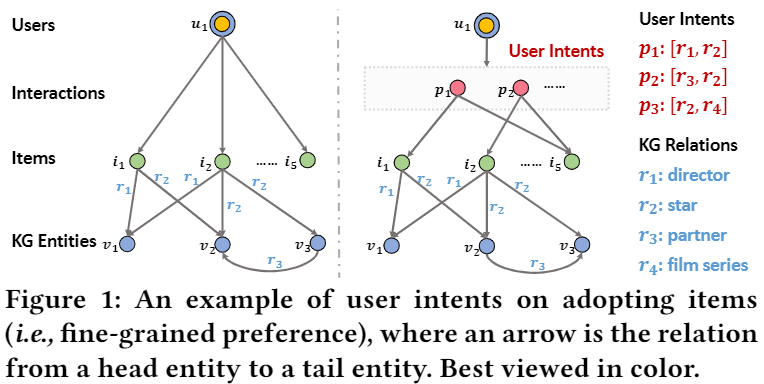
这里其实融入了协同过滤的思想,即采取相同行为的用户拥有相同的特征
Relational Paths:加入知识图谱的过程中,考虑了知识图谱中的relation关系。即更加重视路径的源起和结尾,对于知识图谱中的结构化知识的利用更加充分。图示如下:
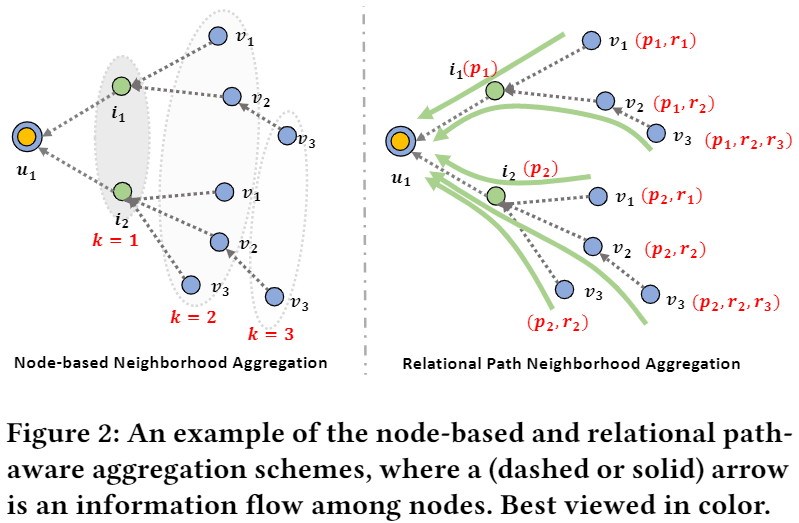
整体模型
主要分为两个部分:
- User Intent Modeling
- Relational Path-aware Aggregation
User Intent Modeling
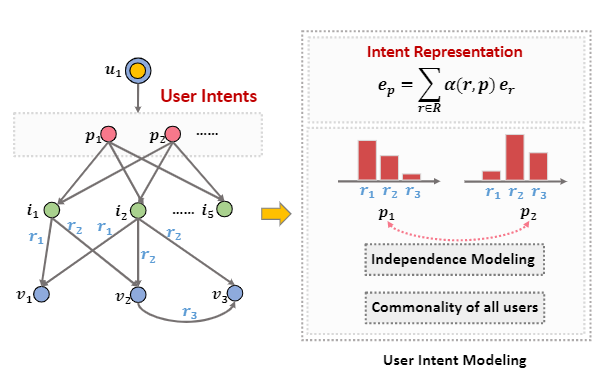
为了增强对于intent的建模的可解释性,对于intent的建模是对知识图谱中所有relation的embedding的注意力加权。具体公式如下: \[ \mathbf{e}_{p}=\sum_{r \in \mathcal{R}} \alpha(r, p) \mathbf{e}_{r} \]
\[ \alpha(r, p)=\frac{\exp \left(w_{r p}\right)}{\sum_{r^{\prime} \in \mathcal{R}} \exp \left(w_{r^{\prime} p}\right)} \]
为了防止intent vector之间重复度过高,需要对intent vector进行Independence Modeling of Intents(正交分解)。从而增强其独立性,是得每一个intent vector都有其存在的意义:使用的是Distance correlation,具体公式如下: \[ \mathcal{L}_{\mathrm{IND}}=\sum_{p, p^{\prime} \in \mathcal{P}, p \neq p^{\prime}} d \operatorname{Cor}\left(\mathbf{e}_{p}, \mathbf{e}_{p^{\prime}}\right) \]
\[ d \operatorname{Cor}\left(\mathbf{e}_{p}, \mathbf{e}_{p^{\prime}}\right)=\frac{d \operatorname{Cov}\left(\mathbf{e}_{p}, \mathbf{e}_{p^{\prime}}\right)}{\sqrt{d \operatorname{Var}\left(\mathbf{e}_{p}\right) \cdot d \operatorname{Var}\left(\mathbf{e}_{p^{\prime}}\right)}} \]
Relational Path-aware Aggregation
通过关系感知的路径构建,我们将得到user和item的向量表示,即:
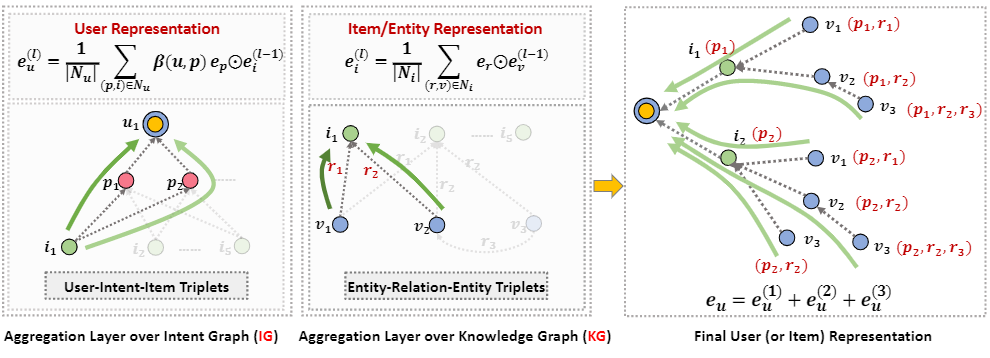
通过公式,我们可以看出:
- Relational Path的构建是通过多层item representation来表示的
- user representation通过item representation来接入relational path
第0层的user, item的表示均是随机初始化的。
得到第一层user的具体过程为: \[ \mathbf{e}_{u}^{(1)}=f_{\mathrm{IG}}\left(\left\{\left(\mathbf{e}_{u}^{(0)}, \mathbf{e}_{p}, \mathbf{e}_{i}^{(0)}\right) \mid(p, i) \in \mathcal{N}_{u}\right\}\right) \]
\[ \mathbf{e}_{u}^{(1)}=\frac{1}{\left|\mathcal{N}_{u}\right|} \sum_{(p, i) \in \mathcal{N}_{u}} \beta(u, p) \mathbf{e}_{p} \odot \mathbf{e}_{i}^{(0)} \]
其中\(\beta(u, p)\)的作用是,每个user对于不同的intent有不同的权重 \[ \beta(u, p)=\frac{\exp \left(\mathbf{e}_{p}^{\top} \mathbf{e}_{u}^{(0)}\right)}{\sum_{p^{\prime} \in \mathcal{P}} \exp \left(\mathbf{e}_{p^{\prime}}^{\top} \mathbf{e}_{u}^{(0)}\right)} \]
\[ \mathbf{e}_{i}^{(1)}=f_{\mathrm{KG}}\left(\left\{\left(\mathbf{e}_{i}^{(0)}, \mathbf{e}_{r}, \mathbf{e}_{v}^{(0)}\right) \mid(r, v) \in \mathcal{N}_{i}\right\}\right) \]
得到第一层item的具体过程为: \[ \mathbf{e}_{i}^{(1)}=f_{\mathrm{KG}}\left(\left\{\left(\mathbf{e}_{i}^{(0)}, \mathbf{e}_{r}, \mathbf{e}_{v}^{(0)}\right) \mid(r, v) \in \mathcal{N}_{i}\right\}\right) \]
\[ \mathbf{e}_{i}^{(1)}=\frac{1}{\left|\mathcal{N}_{i}\right|} \sum_{(r, v) \in \mathcal{N}_{i}} \mathbf{e}_{r} \odot \mathbf{e}_{v}^{(0)} \]
最终为了使路径延伸L层,需要进行L次迭代,具体公式如下: \[ \begin{array}{l} \mathbf{e}_{u}^{(l)}=f_{\mathrm{IG}}\left(\left\{\left(\mathbf{e}_{u}^{(l-1)}, \mathbf{e}_{p}, \mathbf{e}_{i}^{(l-1)}\right) \mid(p, i) \in \mathcal{N}_{u}\right\}\right) \\ \mathbf{e}_{i}^{(l)}=f_{\mathrm{KG}}\left(\left\{\left(\mathbf{e}_{i}^{(l-1)}, \mathbf{e}_{r}, \mathbf{e}_{v}^{(l-1)}\right) \mid(r, v) \in \mathcal{N}_{i}\right\}\right) \end{array} \] 为了展示路径的延伸,将上式中计算\(\mathbf{e}_{i}^{(l)}\)的过程可以展开成如下结果: \[ \mathbf{e}_{i}^{(l)}=\sum_{s \in \mathcal{N}_{i}^{l}} \frac{\mathbf{e}_{r_{1}}}{\left|\mathcal{N}_{s_{1}}\right|} \odot \frac{\mathbf{e}_{r_{2}}}{\left|\mathcal{N}_{s_{2}}\right|} \odot \cdots \odot \frac{\mathbf{e}_{r_{l}}}{\left|\mathcal{N}_{s_{l}}\right|} \odot \mathbf{e}_{s_{l}}^{(0)} \]
模型训练
模型预测
为了防止过平滑,需要将每一层的计算结构进行叠加: \[ \mathbf{e}_{u}^{*}=\mathbf{e}_{u}^{(0)}+\cdots+\mathbf{e}_{u}^{(L)}, \quad \mathbf{e}_{i}^{*}=\mathbf{e}_{i}^{(0)}+\cdots+\mathbf{e}_{i}^{(L)} \] 最后的预测指标为向量间的点积: \[ \hat{y}_{u i}=\mathbf{e}_{u}^{* \top} \mathbf{e}_{i}^{*} \]
模型优化
总的Loss为: \[ \mathcal{L}_{\mathrm{KGIN}}=\mathcal{L}_{\mathrm{BPR}}+\lambda_{1} \mathcal{L}_{\mathrm{IND}}+\lambda_{2}\|\Theta\|_{2}^{2} \] 其中预测结果使用BPR Loss(使得正样本和负样本之间的差距尽可能大): \[ \mathcal{L}_{\mathrm{BPR}}=\sum_{(u, i, j) \in O}-\ln \sigma\left(\hat{y}_{u i}-\hat{y}_{u j}\right) \] IND Loss为之前提到的intent 正交化的Loss: \[ \mathcal{L}_{\mathrm{IND}}=\sum_{p, p^{\prime} \in \mathcal{P}, p \neq p^{\prime}} d \operatorname{Cor}\left(\mathbf{e}_{p}, \mathbf{e}_{p^{\prime}}\right) \]
实验结果
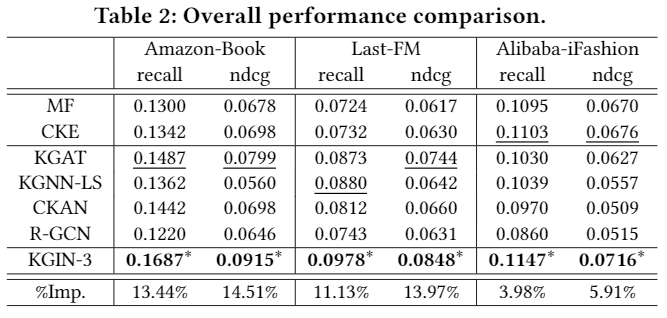
消融实验


参数敏感性实验
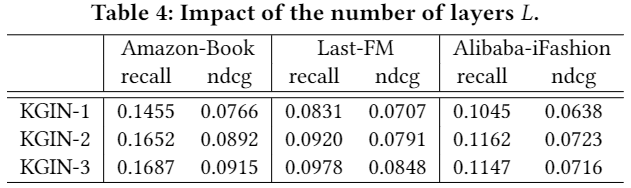
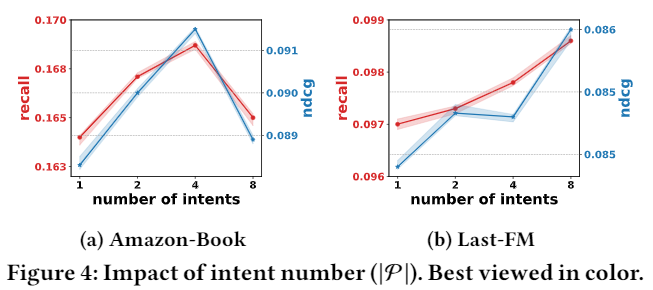
(KGIN)Learning Intents behind Interactions with Knowledge Graph for Recommendation 论文笔记