chap 8-Evaluation in information retrieval

信息检索的评价

信息系统测试集的组成：

1. 一个文档集
2. 一组用于测试的信息需求集合，信息需求可以表示为查询（信息系统!=查询词）
3. 一组相关性测试结果，对于每个查询-文档而言，赋予一个二值判断结果（相关、不相关）

对无序检索结果集合的评价

正确率：

\[\text { Precision }=\frac{\text { 返回结果中相关文档的数目 }}{\text { 返回结果的数目 }}=P(\text { relevant } \mid \text { retrieved })\]

召回率：

\[\text { Recall }=\frac{\text { 返回结果中相关文档的数目 }}{\text { 所有相关文档的数目 }}=P(\text { retrieved } \mid \text { relevant })\]

精确率：

\[\text { Recall }=\frac{\text { 返回结果中真正例+正反例 }}{\text { 所有被判断的文档的数目 }}\]

精确率往往导致不准确的结果：绝大多数情况下，信息检索中的数据存在着极度的不均衡性，比如通常情况下，超过 99.9%的文档 都是不相关文档。这样的话，一个简单地将所有的文档都判成不相关文档的系统就会获得非常 高的精确率值，从而使得该系统的效果看上去似乎很好。而即使系统实际上非常好

正确率+召回率（F值）：

\[F=\frac{1}{\alpha \frac{1}{P}+(1-\alpha) \frac{1}{R}}\]

可以通过调整\[\alpha\]来控制正确率和召回率的权重

对有序检索结果的评价

相比于无序检索结果，有序检索结果只对top-K个返回的结果进行处理

正确率-召回率曲线：

随着K的增加，出现锯齿形图案

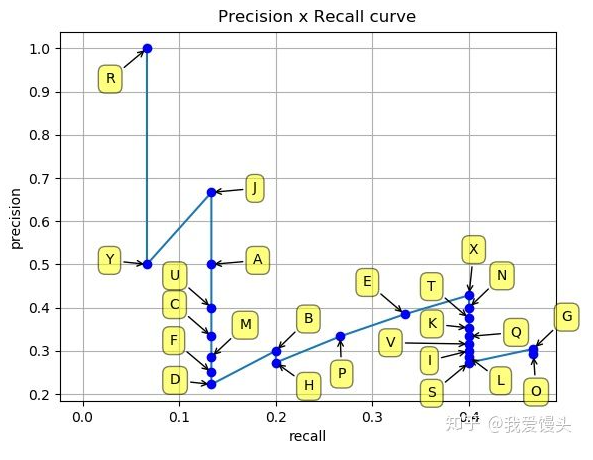
插值正确率：

起到平滑的作用，具体做法为：对每一个Precision值，使用其右边最大的Precision值替代

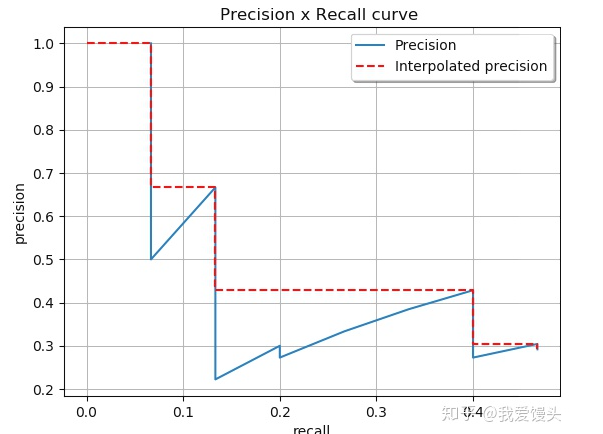
11点插值平均正确率：

对平滑后的Precision曲线进行均匀采样出11个点（每个点间隔0.1），然后计算这11个点的平均Precision

\[A P=\frac{1}{11} \times\left(A P_{r}(0)+A P_{r}(0.1)+\ldots+A P_{r}(1.0)\right)\]

平均正确率均值MAP（Mean Average Precision）：

目前普遍使用，具有较好的稳定性和代表性

• 平均正确率AP：在每个相关文档位置上正确率的平均值

  某个查询Q共有6个相关结果，某系统排序 返回了5篇相关文档，其位置分别是第1，第2，第5，第 10，第20位，则AP=(1/1+2/2+3/5+4/10+5/20+0)/6；其中1/1，2/2，3/5等就是平均正确率

• 平均正确率均值MAP：对一组查询的top-K个返回结果求平均正确率

  \[\operatorname{MAP}(Q)=\frac{1}{|Q|} \sum_{j=1}^{|Q|} \frac{1}{m_{j}} \sum_{k=1}^{m_{j}} \operatorname{Precision}\left(R_{j k}\right)\]

相关性判定

在构建测试集时，需要：

1. 设计用于测试的查询
2. 需要判定文档的相关性

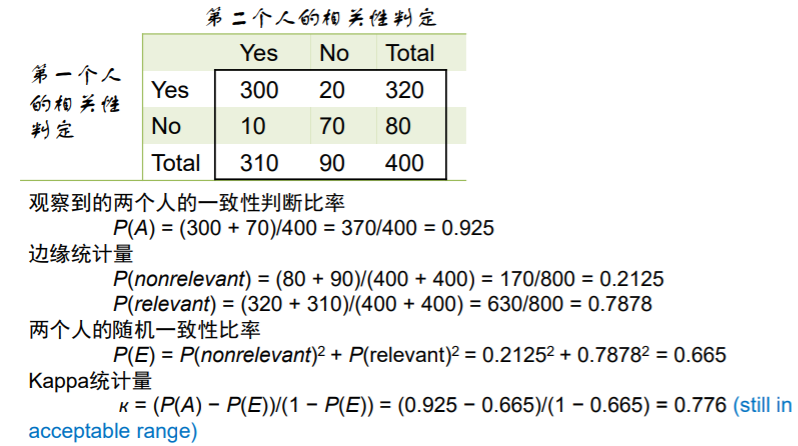
此处主要讨论判定文档的相关性，即考虑雇佣多个人来进行相关性判定，所需要做的是判定多个人之间的判定是否一致，采用kappa统计量，即：

\[\text {kappa}=\frac{P(A)-P(E)}{1-P(E)}\]

其中P(A)是观察到的一致性判断比率，p(E)是比较对象间的随机一致性比率，距离如下：

reference

[1] 白话mAP

[2] 中科大课件