卷积神经网络——pytorch-learning(四)
图像形成简述
一般图像分为两类:
栅格图像:图像由像素点组成,一般可以由人工捕获,在相机摄像时,每个像素点都通过一个光学元件来采集——放大后变成马赛克
矢量图像:一般无法人工捕获,由程序生成,相当于一段描述:圆心在哪,半径多少....,一般由程序画出来,而不是现成的——放大不变形
卷积神经网络简述
使用DNN(全连接神经网络)来进行图像分类时,是将二维图像完全展开成一维图像,只保留了像素间横向的联系,却忽略了纵向的联系。
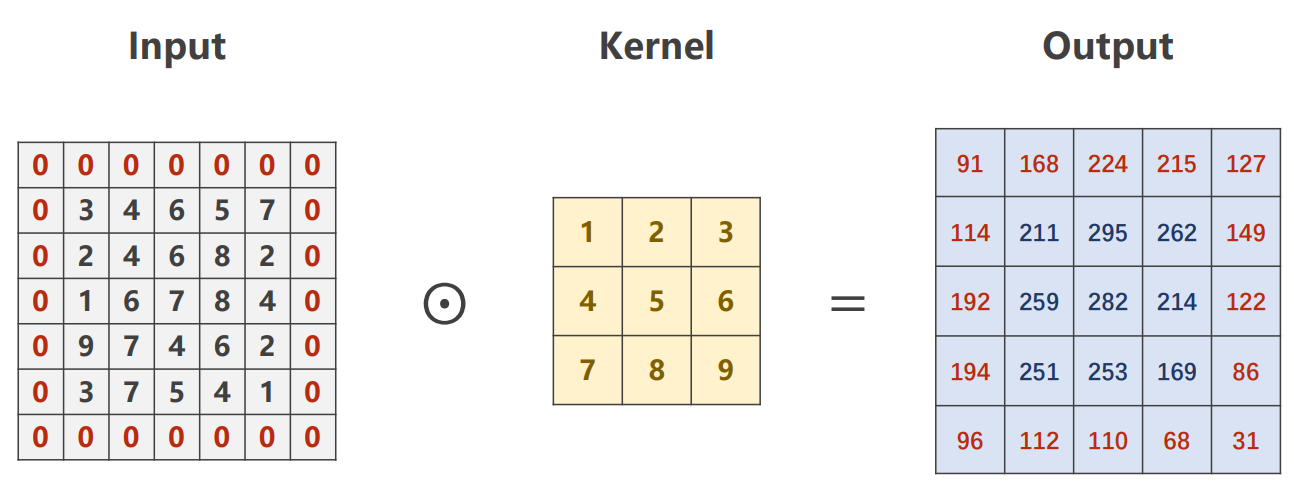
因此我们引入了卷积神经网络,提取其二维特征,其工作过程是通过黄色的卷积核来提取绿色的图像中的二维特征,随后将特征输出到粉色矩阵中,以便进行下一步的处理。单通道卷积的运算过程如下所示:
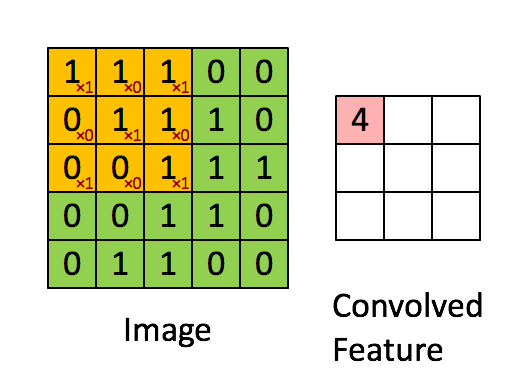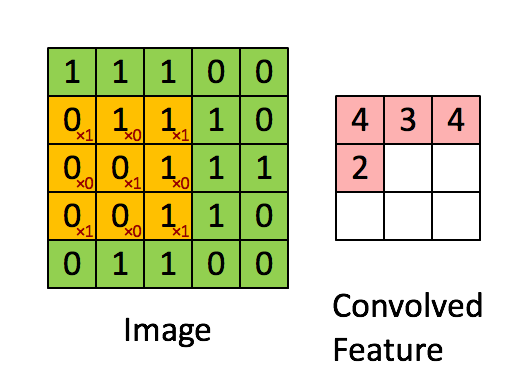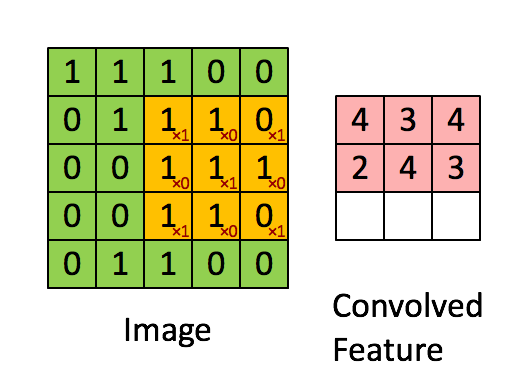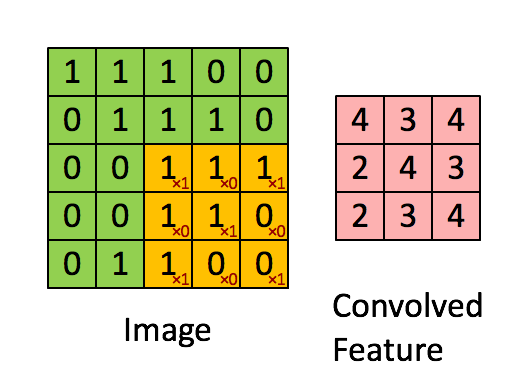
对于卷积核作用的直观理解:检测图像的局部是否满足某一特征,如果满足,则返回一个较大的值;否则返回一个较小的值
注意:对于多通道的图像,每次卷积是针对所有的通道来进行的,卷积核应该是三维的,第三个维度的大小应该和通道数相同,因此在讨论卷积核的大小时,只考虑二维的大小。如下图所示:
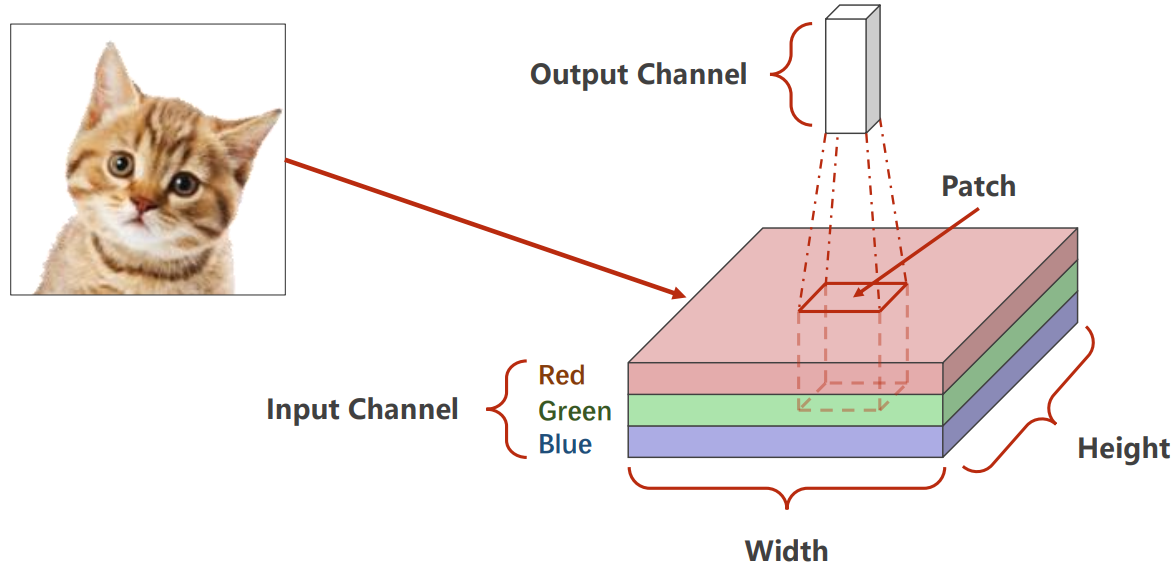
展开后具体如下:
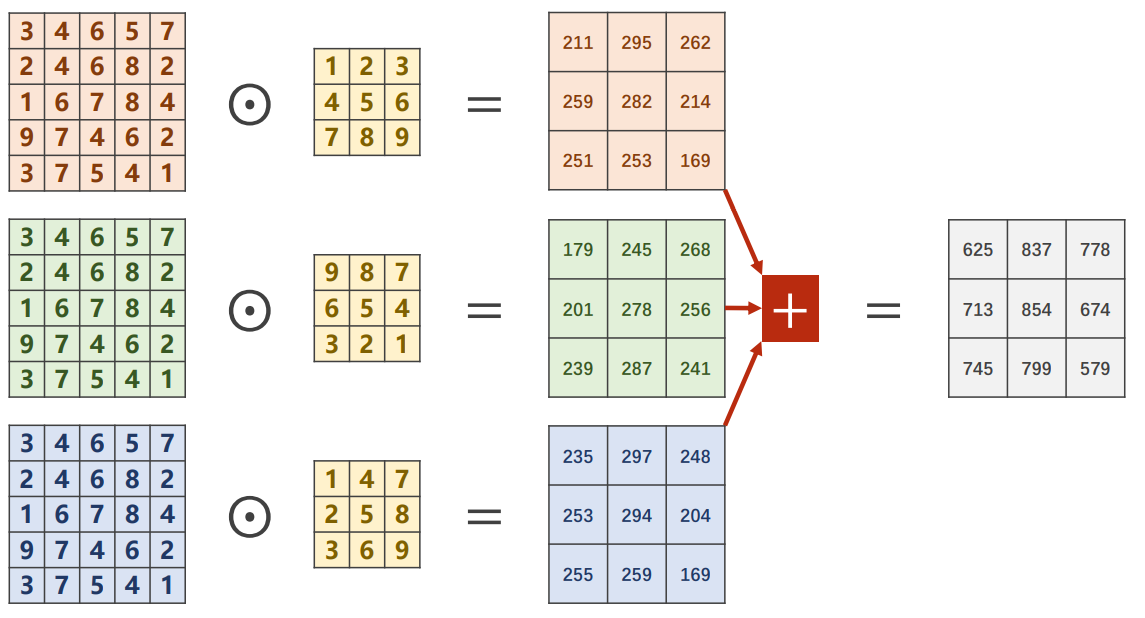
压缩后如下所示(卷积时不加padding):
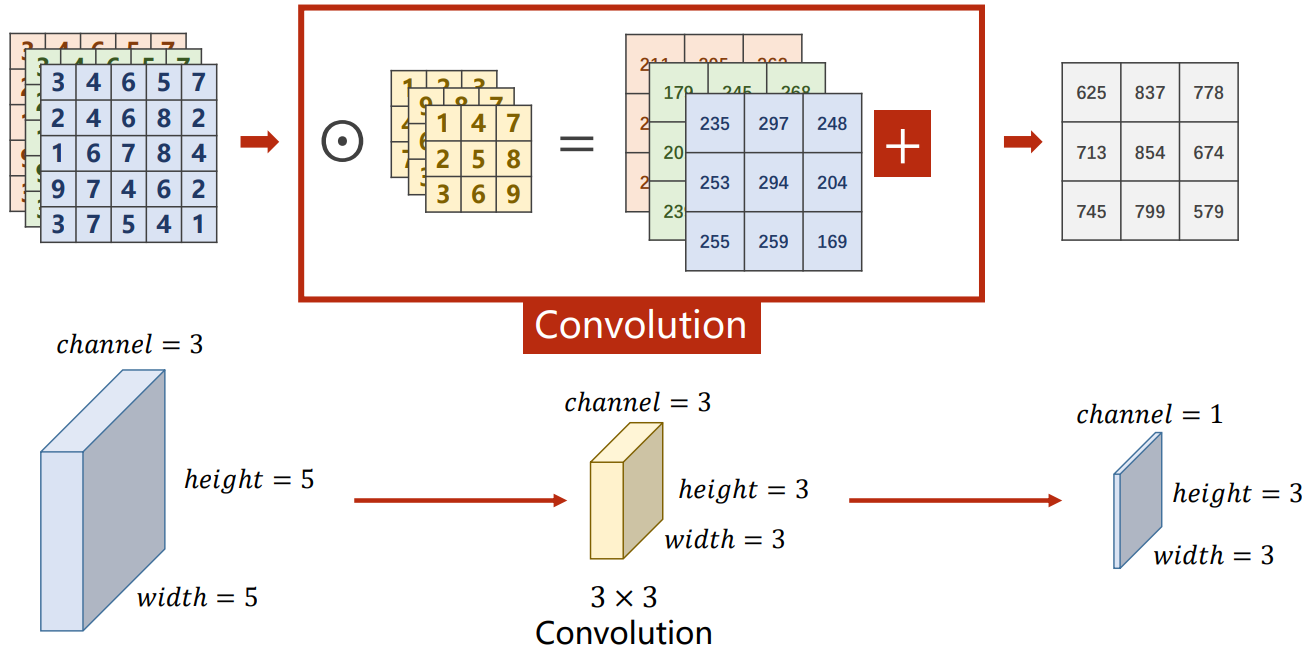
泛化图像的尺寸,以及投影到多个卷积核之后可以得到:
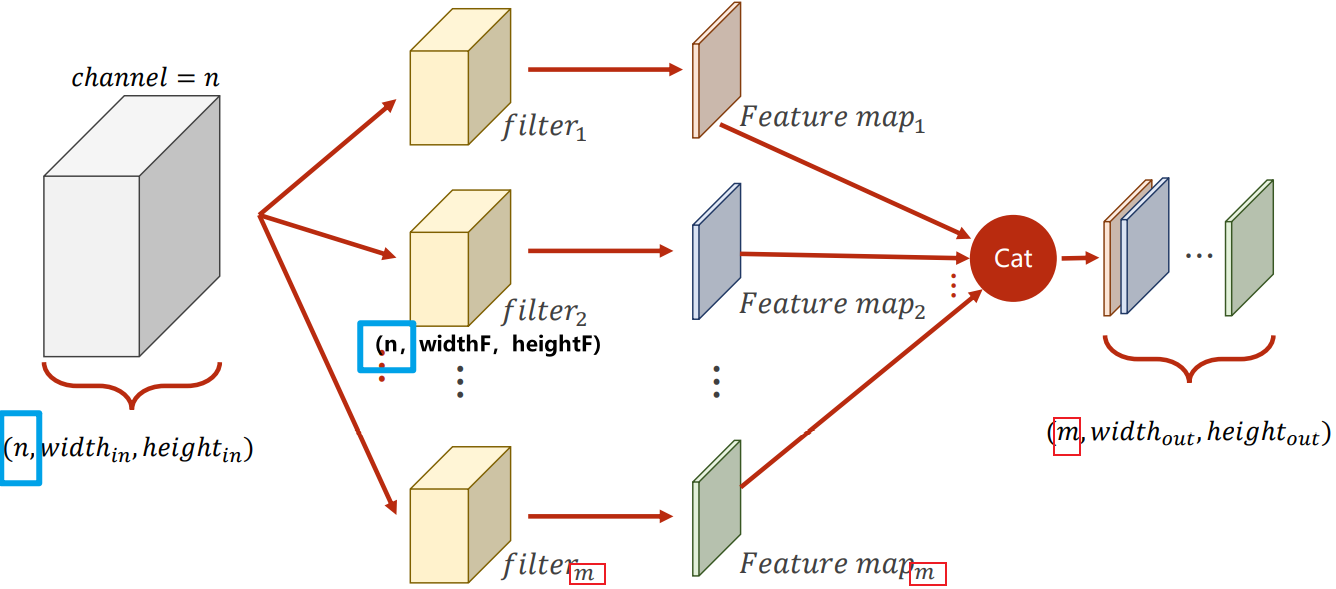
注意:卷积核的数目与输出结果的通道数相同
卷积核的相关参数
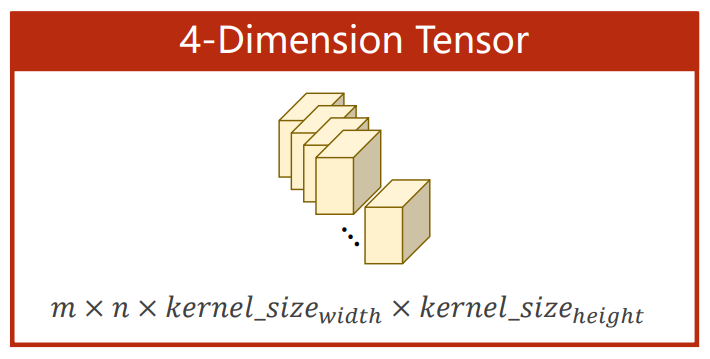
其中:
- m是卷积核的个数
- n是输入图像的通道数
padding
在图像外层填充0,借此来保证经过卷积计算后的图形与原图形大小保持一致。一般而言,外围填充的0的圈数为
如下图所示:
stride
在进行卷积运算时,每一次移动卷积核的距离
1 | import torch |

Pooling
可以理解成下采样,用来筛选特征,压缩图像大小。但是特征筛选只在同一个通道内进行;经过pooling之后图像的通道数不改变;在pooling层中:
stride = kernal_size
- Max Pooling:每次取局部内的最大值
1 | import torch |

代码示例
在此处我们使用MNIST数据集作为演示,具体网络架构如下:
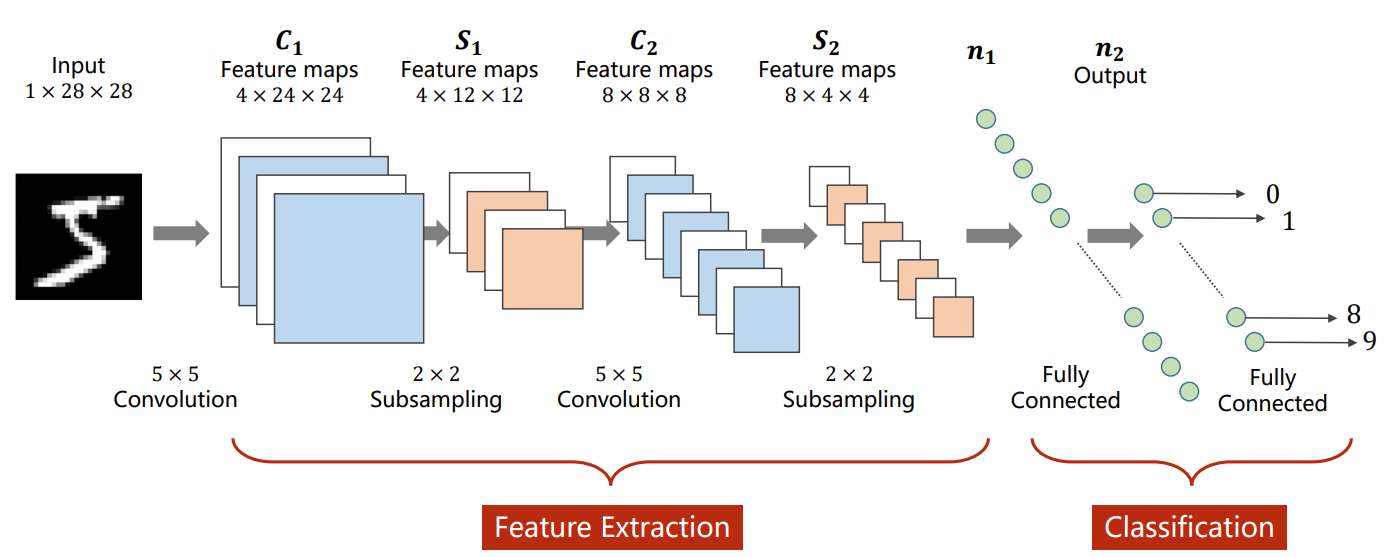
注意:卷积层和池化层不在意图像的大小,但是线性层在意,需要提前计算
1 | class Net(torch.nn.Module): |
对于GPU的使用:
1 | # 选择设备 |
卷积神经网络进阶
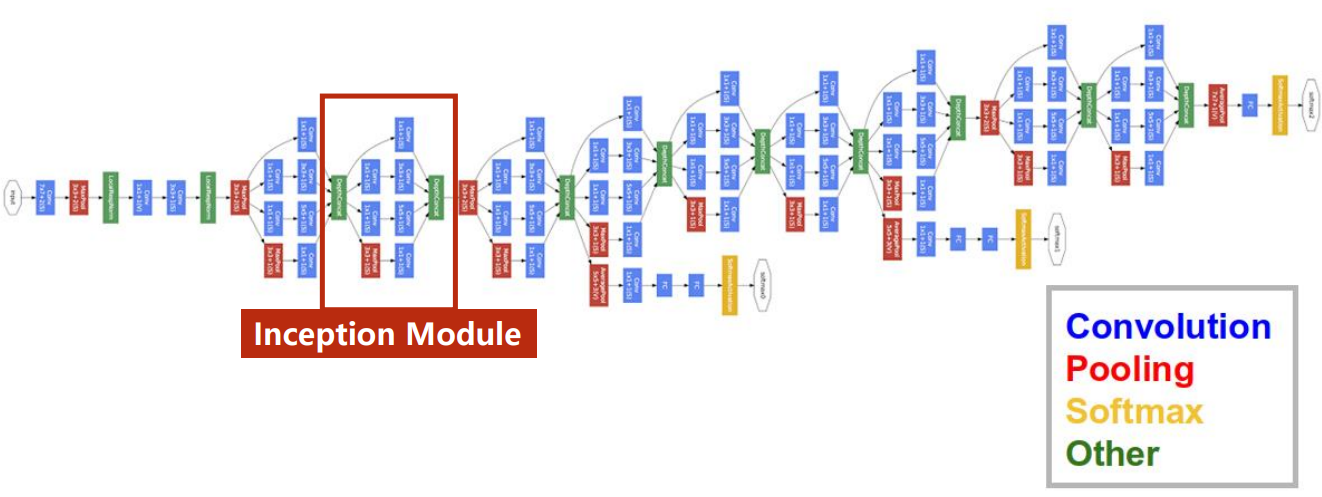
以复杂网络GoogLeNet为例子
对Inception模块进行解释
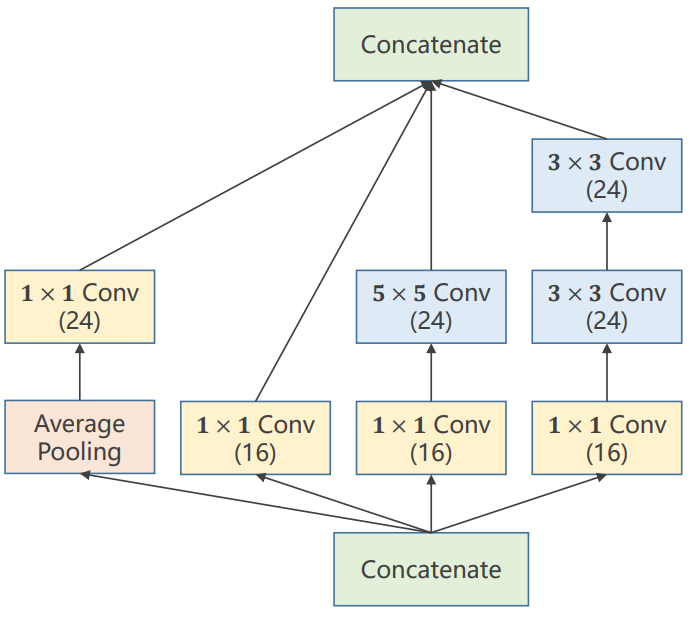
1*1的卷积核
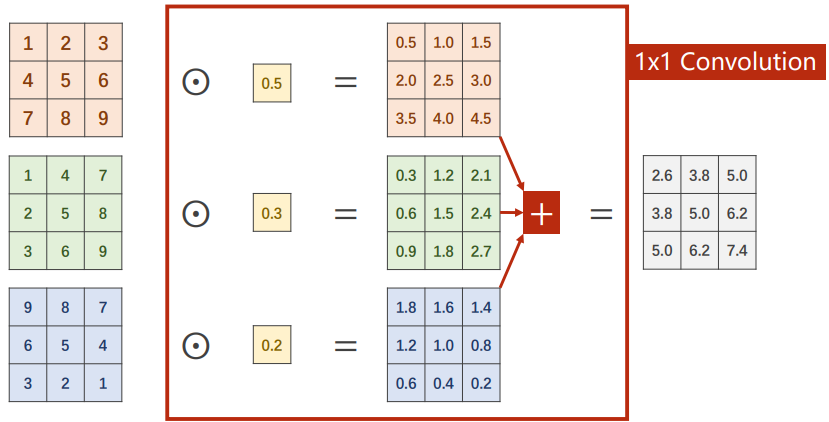
作用:
将所有输入通道同一像素点的数值进行加权
改变通道的数目,相比于其他大小的卷积,1*1的卷积在改变通道数目时,计算量较小。对比如下:
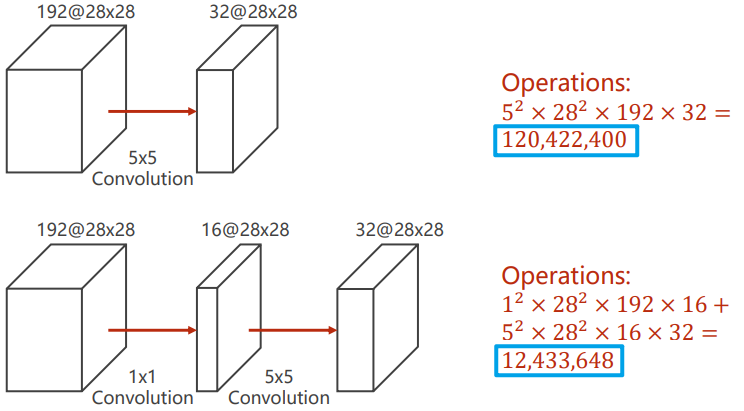
代码实现
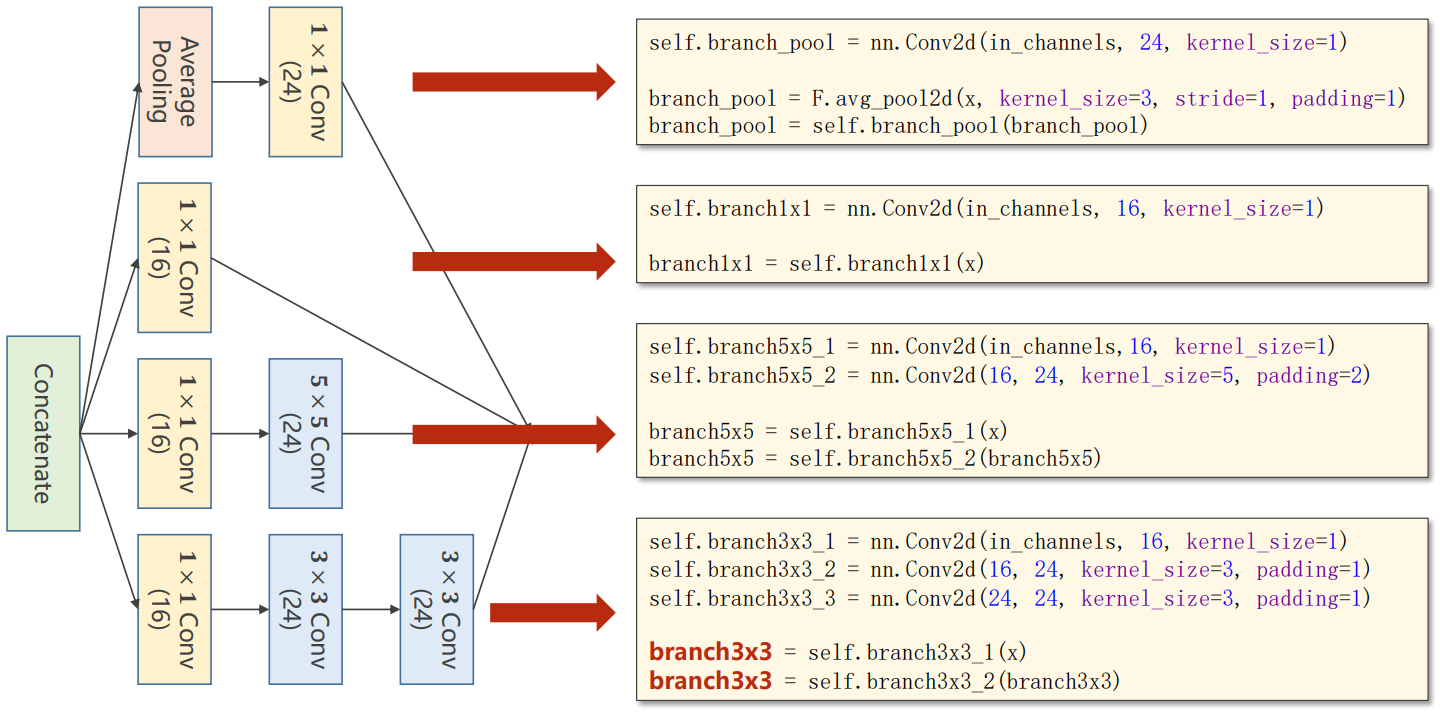
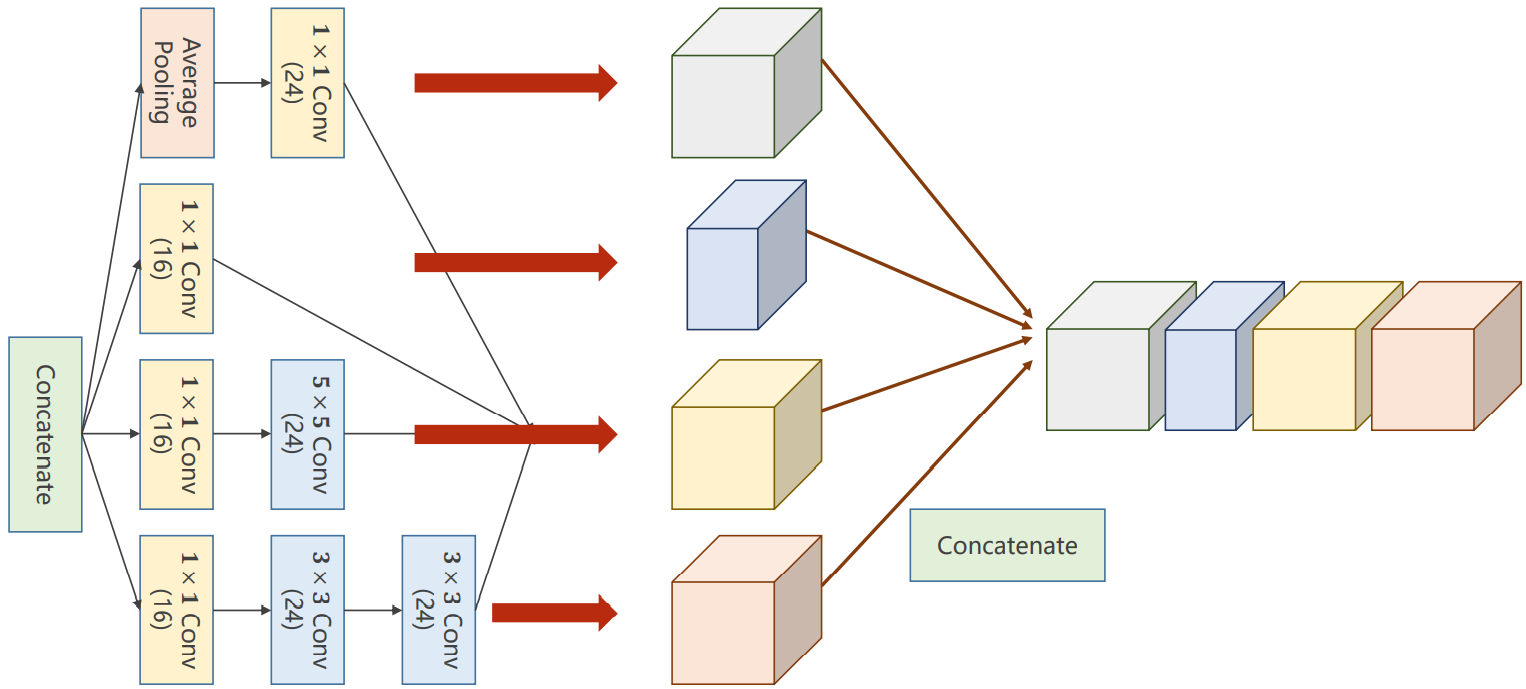
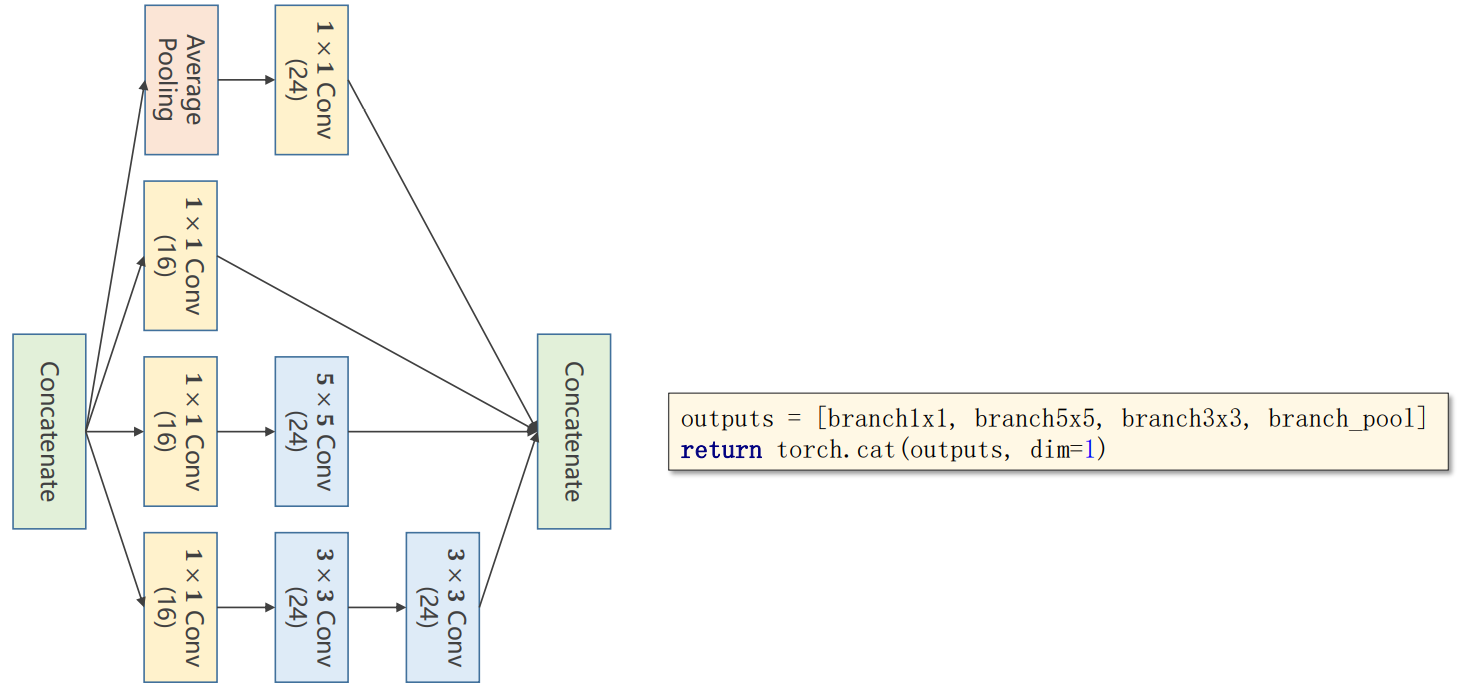
注意:张量的维度表示方式为(B,C,W,H),因此torch.cat操作时dim=1
卷积的深度及其效果
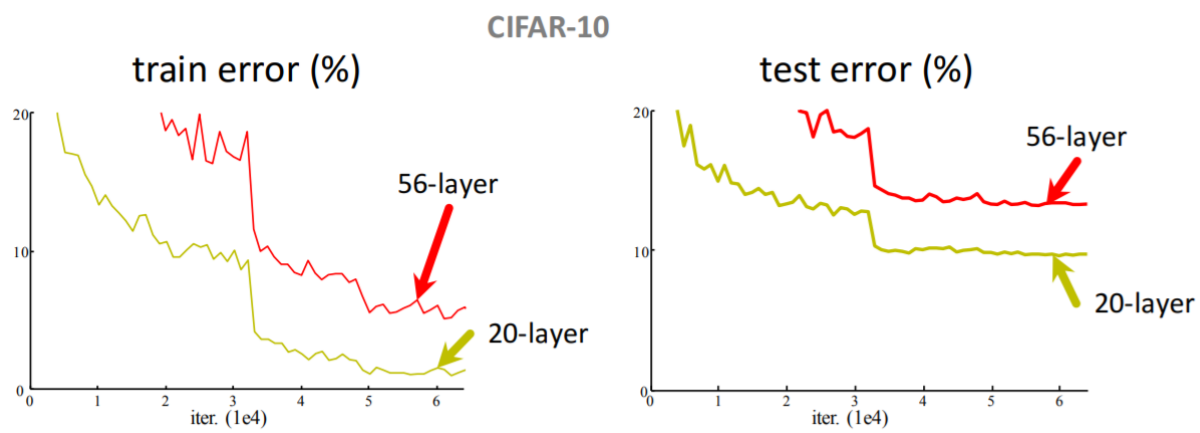
结论:并不是卷积越深,效果越好
解决方法:使用残差网络(Residual net)
残差网络(Residual net)
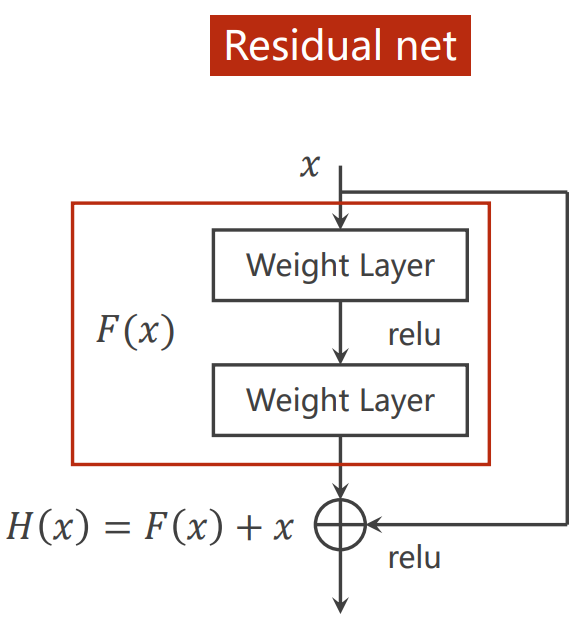
## 搭建网络的建议
- 逐层搭建,逐层测试,主要测试网络的输入与输出的矩阵的大小

引用
[1] 河北工业大学刘洪普老师的视频教程
[2] He K, Zhang X, Ren S, et al. Identity Mappings in Deep Residual Networks
[3] Huang G, Liu Z, Laurens V D M, et al. Densely Connected Convolutional Networks
卷积神经网络——pytorch-learning(四)