发表更新pytorch-learning12 分钟读完 (大约1815个字)0次访问

Logistic回归与多分类问题——pytorch-learning（三）

Logistic回归

基本概念

Logistic回归是将实数范围映射的值到[0,1]的范围内，虽然是回归模型，但是常被用作分类任务，理解成是否属于某一类别的概率，其映射又公式称为sigmoid函数，如下：

\[\sigma(x)=\frac{1}{1+e^{-x}}\]

优化的目标函数也应该相应做出改变，改为使用交叉熵函数cross-entropy，其含义是计算两个概率分布之间的差异性，越小越好，具体公式展示如下：

\[H(p, q)=\sum_{i} p\left(x_{i}\right) \log \frac{1}{\log q\left(x_{i}\right)}=-\sum_{i} p\left(x_{i}\right) \log q\left(x_{i}\right)\]

在二分类问题中，具体应用如下：

\[\operatorname{los} s=-(y \log \hat{y}+(1-y) \log (1-\hat{y}))\]

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import torch.nn.functional as F

x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
#-------------------------------------------------------#
class LogisticRegressionModel(torch.nn.Module):
	def __init__(self):
		super(LogisticRegressionModel, self).__init__()
		self.linear = torch.nn.Linear(1, 1)
        
	def forward(self, x):
		y_pred = F.sigmoid(self.linear(x))
		return y_pred
    
model = LogisticRegressionModel()
#-------------------------------------------------------#
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
#-------------------------------------------------------#
for epoch in range(1000):
	y_pred = model(x_data)
	loss = criterion(y_pred, y_data)
	print(epoch, loss.item())
    
	optimizer.zero_grad()
	loss.backward()
	optimizer.step()

多维特征值问题

假设输入8维，输出1维

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        ## 输入特征4维，输出特征1维
        self.linear = torch.nn.Linear(4,2)
        ## 此时对同一组2维数据中的每一个取sigmoid
        self.sigmoid = torch.nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        print(x1)
        x2 = self.sigmoid(x1)
        print(x2)
        return x2

model = Model()

x_data = torch.Tensor([[1.0,2.0,3.0,4.0],[1.5,2.5,3.5,4.5]])
y_predic = model(x_data)

结果如下：

多层神经网络

如上所示，在多层神经网络中，一般利用torch.nn.Linear进行升维或降维，即：

将上图的神经网络实现成代码，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
## 数据读取
import numpy as np
import torch

# 读取成numpy格式，注意一般gpu只接受32位，分隔符按照数据的内容自己选定
xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)

# from_numpy可以自动转化为Tensor格式
x_data = torch.from_numpy(xy[:,:-1])
y_data = torch.from_numpy(xy[:, [-1]])


## 设计网络
class Model(torch.nn.Module):
	def __init__(self):
		super(Model, self).__init__()
		self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.sigmoid = torch.nn.Sigmoid()
        
    def forward(self, x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x
    
model = Model()

## 构造损失和优化函数


## 进行迭代
for epoch in range(100): 
    # Forward
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())
    # Backward
    optimizer.zero_grad()
    loss.backward()
    # Update
    optimizer.step()

以上代码有两个问题：

  1. 每个epoch计算的是全部的数据，而不是mini-batch的
  2. 目前的代码均只使用了sigmoid作为激活函数

接下来我们尝试解决这两个问题：

首先，用ReLu替换sigmoid作为激活函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import torch

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.relu = torch.nn.ReLU()
        self.sigmoid = torch.nn.Sigmoid()
    
    def forward(self, x):
        x = self.relu(self.linear1(x))
        x = self.relu(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x

model = Model()

注意：使用ReLu时，为防止最后的输出值被用来计算ln，所以最后一层用sigmoid作为激活函数

接下来，我们研究如何利用mini-batch来加载数据集

数据加载问题

主要工具理解

主要使用Dataset和DataLoader这两个工具，其中：

  • Dataset：负责根据下标取出数据
  • DataLoader：对Dataset进行包裹，负责取出mini-batch大小的数据

涉及的概念：

  • iteration：表示1次迭代（也叫training step），每次迭代更新1次网络结构的参数，所需的数据量为1个batch的大小
  • batch-size：1次迭代所使用的样本量
  • epoch：1个epoch表示过了1遍训练集中的所有样本（包含多个batch的数据）

若总的数据量为1000，batch的大小为100，则每一次经过一次epoch，需要通过10次iteration

代码展示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import torch

## 注意Dataset为抽象类，而DataLoader不是
from torch.utils.data import Dataset
from torch.utils.data import DataLoader

class DiabetesDataset(Dataset):
    def __init__(self):
        ## 1.一次加载所有数据，按下标存取
        ## 2.只加载文件名
        pass
    	
    def __getitem__(self, index):
        ## 如果初始化时读取的是文件名，则这里开始根据文件名读入文件
        pass
    
    def __len__(self):
        pass

dataset = DiabetesDataset()
train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=2)

num_workers的含义：读取数据的并行进程的数目

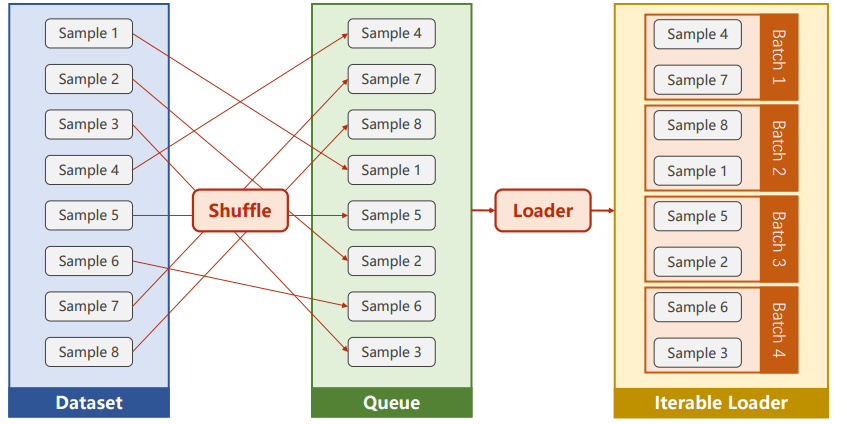
对于参数shuffle的理解：

注意：windows和linux系统上训练数据的差别，因为两个系统实现多线程的方式不同，windows使用spawn来代替fork

  • windows：

    1
    2
    3
    4
    5
    6
    7
    train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=2)
    ……
    # 不能让for循环直接打头
    if __name__ == '__main__':
        for epoch in range(100):
            for i, data in enumerate(train_loader, 0):
                ……

  • linux：

    1
    2
    3
    4
    5
    train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=2)
    ……
    for epoch in range(100):
    	for i, data in enumerate(train_loader, 0):
    		……

Dataset的实现（以加载全部数据为例）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class DiabetesDataset(Dataset):
    def __init__(self, filepath):
        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
        self.len = xy.shape[0]
        self.x_data = torch.from_numpy(xy[:, :-1])
        self.y_data = torch.from_numpy(xy[:, [-1]])
        
    def __getitem__(self, index):
        ## 返回下标元组
    	return self.x_data[index], self.y_data[index]
    
    def __len__(self):
    	return self.len

dataset = DiabetesDataset('diabetes.csv.gz')
train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=2)

......

## 使用数据加载器后的训练流程的变化
for epoch in range(100):
    ## 此处使用mini-batch，batch-size为32，每次迭代只使用一个数据
    for i, data in enumerate(train_loader, 0):
        # 1. Prepare data（dataLoader会自动将数据转化为Tensor）
        inputs, labels = data
        # 2. Forward
        y_pred = model(inputs)
        loss = criterion(y_pred, labels)
        print(epoch, i, loss.item())
        # 3. Backward
        optimizer.zero_grad()
        loss.backward()
        # 4. Update
        optimizer.step()

多分类问题

softmax分类器

在多分类问题中，我们期望的输出时当前数据属于各个类别的概率分布，因此我们期望它满足如下的条件：

  1. \[P(y=i) \geq 0\]
  2. \[\sum_{i=0}^{n} P(y=i)=1\]

因此，人们提出了如下的模型：

\[P(y=i)=\frac{e^{z_{i}}}{\sum_{j=0}^{K-1} e^{z_{j}}}, i \in\{0, \ldots, K-1\}\]

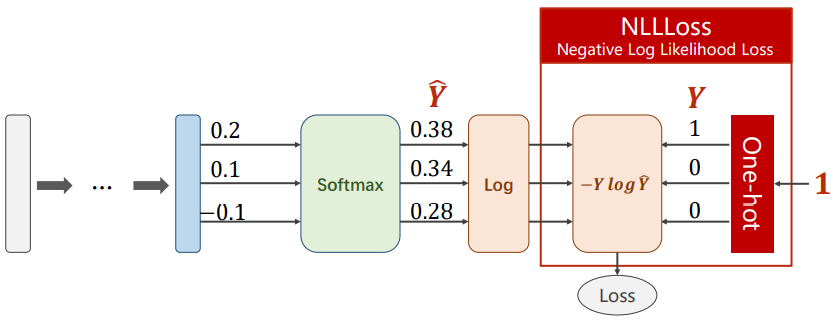
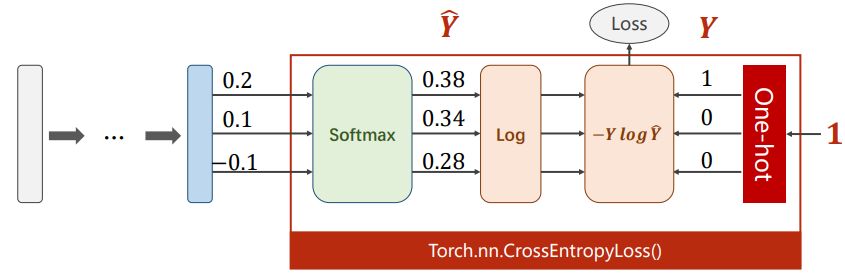
注意：在pytorch中，Cross-Entropy Loss与negative Log Likelihood Loss之间的区别

引用在pytorch论坛中看到的一句话：

If you apply Pytorch’s CrossEntropyLoss to your output layer, you get the same result as applying Pytorch’s NLLLoss to a LogSoftmax layer added after your original output layer.

对比示意图如下所示（均会自动将类别标签转化成one-hot向量）：

代码验证：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import torch

# Y是长整型的张量
Y = torch.LongTensor([2, 0, 1])
Y_pred1 = torch.Tensor([[0.1, 0.2, 0.9],[1.1, 0.1, 0.2],[0.2, 2.1, 0.1]])
Y_pred2 = torch.Tensor([[0.8, 0.2, 0.3],[0.2, 0.3, 0.5],[0.2, 0.2, 0.5]])

# 
criterion1 = torch.nn.CrossEntropyLoss()
l1 = criterion1(Y_pred1, Y)
l2 = criterion1(Y_pred2, Y)
print("Batch Loss1 = ", l1.data, "\nBatch Loss2=", l2.data)
#
actFunction = torch.nn.Softmax()
r1 = torch.log(actFunction(Y_pred1))
r2 = torch.log(actFunction(Y_pred2))
criterion2 = torch.nn.NLLLoss()
r1 = criterion2(r1, Y)
r2 = criterion2(r2, Y)
print("Batch Loss1 = ", r1.data, "\nBatch Loss2=", r2.data)

结果如下：

引用

[1] 河北工业大学刘洪普老师的视频教程

Logistic回归与多分类问题——pytorch-learning（三）

https://xdren69.github.io/2020/08/01/pytorch-learning-3/

作者

Xdren

发布于

2020-08-01

更新于

2021-03-01

许可协议

#

评论

关注我

链接

分类

最新文章

归档

标签

Data Structure1
GNN1
Hexo,Icarus1
NLP6
Python1
RL1
binary search1
cuda1
datawhale5
deep learning4
disjoint set1
entity disambiguation1
item recommendation3
knowledge graph3
news recommendation5
pytorch4
review-based recommendation1
text representation1
×