线性回归——pytorch-learning（二）

线性模型

假设我们的线性模型的格式为：

\[\hat{y}=x * \omega\]

先确定优化目标，也就是cost function，我们算则MSE（Mean Square Error）

\[\cos t=\frac{1}{N} \sum_{n=1}^{N}\left(\hat{y}_{n}-y_{n}\right)^{2}\]

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# 前向传播
def forward(x):
return x * w

# 计算loss，评价模型
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)

w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1): #对参数进行穷举
	print('w=', w)
	l_sum = 0
	for x_val, y_val in zip(x_data, y_data):
		y_pred_val = forward(x_val)
		loss_val = loss(x_val, y_val)
		l_sum += loss_val
		print('\t', x_val, y_val, y_pred_val, loss_val)
	print('MSE=', l_sum / 3)
	w_list.append(w)
	mse_list.append(l_sum / 3)

注：可以用visdom进行实时绘图，对数据进行可视化

梯度下降算法

我们将寻找使目标函数值最小的参数的问题称为优化问题，为了代替对于参数的遍历方法，引入梯度下降算法

\[\omega=\omega-\alpha \frac{\partial \cos t}{\partial \omega}\]

更新公式的方法

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0

def forward(x):
	return x * w

def cost(xs, ys):
	cost = 0
	for x, y in zip(xs, ys):
		y_pred = forward(x)
		cost += (y_pred - y) ** 2
	return cost / len(xs)

def gradient(xs, ys):
	grad = 0
	for x, y in zip(xs, ys):
		grad += 2 * x * (x * w - y)
	return grad / len(xs)

print('Predict (before training)', 4, forward(4))
for epoch in range(100):
	cost_val = cost(x_data, y_data)
	grad_val = gradient(x_data, y_data)
	w -= 0.01 * grad_val
	print('Epoch:', epoch, 'w=', w, 'loss=', cost_val)
print('Predict (after training)', 4, forward(4))

关于梯度下降，以上使用的是普通的梯度下降：即用所有数据的平均损失值来进行梯度更新；我们也可以使用SGD（Stochastic Gradient Descent）：即随机使用一个数据来更新梯度。SGD的好处是：单个样本包含了随机噪声，这样就避免停留在鞍点，缺点是：时间效率太低；因此现在主流是每次将训练数据分为过个batch，没经过一个batch进行一次数据更新

反向传播

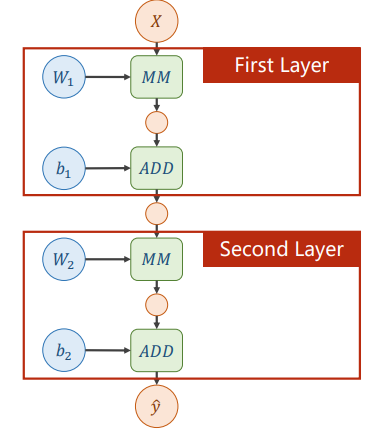
本质是构建计算图，以两层神经网络为例：

\[\hat{y}=W_{2}\left(W_{1} \cdot X+b_{1}\right)+b_{2}\]

其计算图为：

pytorch基础

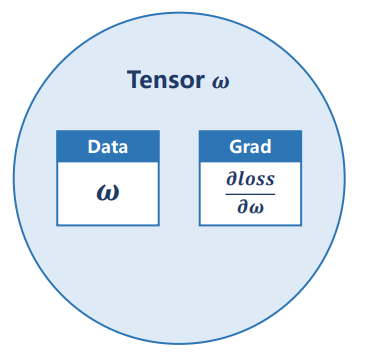
• Tensor：一般针对每一个权重或中间变量使用一个tensor，其内部组成如下：包含权重本身和梯度（也是一个Tensor）两个部分

注意：

• 每进行一次反向传播，计算图就会被释放！

• Tensor在做加法运算时会构建计算图；如过不进行backward()，就一直不会释放；

• Tensor中的梯度在.backward()方法执行后会被累加，所以每次在更新完梯度后都需要，将梯度清零

• 在进行计算时应使用w.grad.data，而不是w.grad（Tensor），否则会产生新的计算图

print("predict (before training)", 4, forward(4).item())
for epoch in range(100):
	for x, y in zip(x_data, y_data):
		l = loss(x, y)
		l.backward() #释放计算图，累加梯度
		print('\tgrad:', x, y, w.grad.item())
		w.data = w.data - 0.01 * w.grad.data #更新梯度
		w.grad.data.zero_() #梯度清零
	print("progress:", epoch, l.item())
print("predict (after training)", 4, forward(4).item())

用pytorch实现线性回归

import torch
# 准备数据
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])

# 设计计算图（根据上一篇）
class LinearModel(torch.nn.Module): 
    # 通过继承moudle，自动计算backword
	def __init__(self):
		super(LinearModel, self).__init__()
		self.linear = torch.nn.Linear(1, 1)
        # Class nn.Linear contain two member Tensors: weight and bias
        
	def forward(self, x):
		y_pred = self.linear(x)
		return y_pred

model = LinearModel()

关于torch.nn.Linear，官方文档如下：

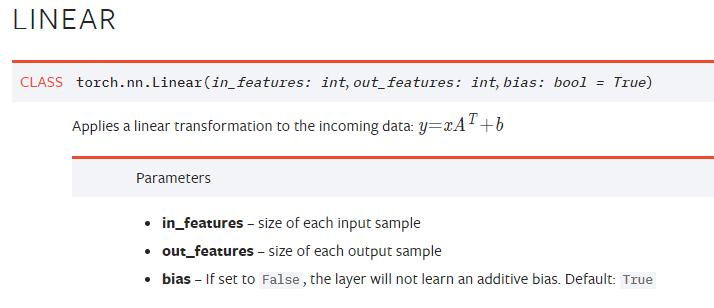
优化目标函数MSE如下所示：

criterion = torch.nn.MSELoss(size_average=False)

其中官方文档为：

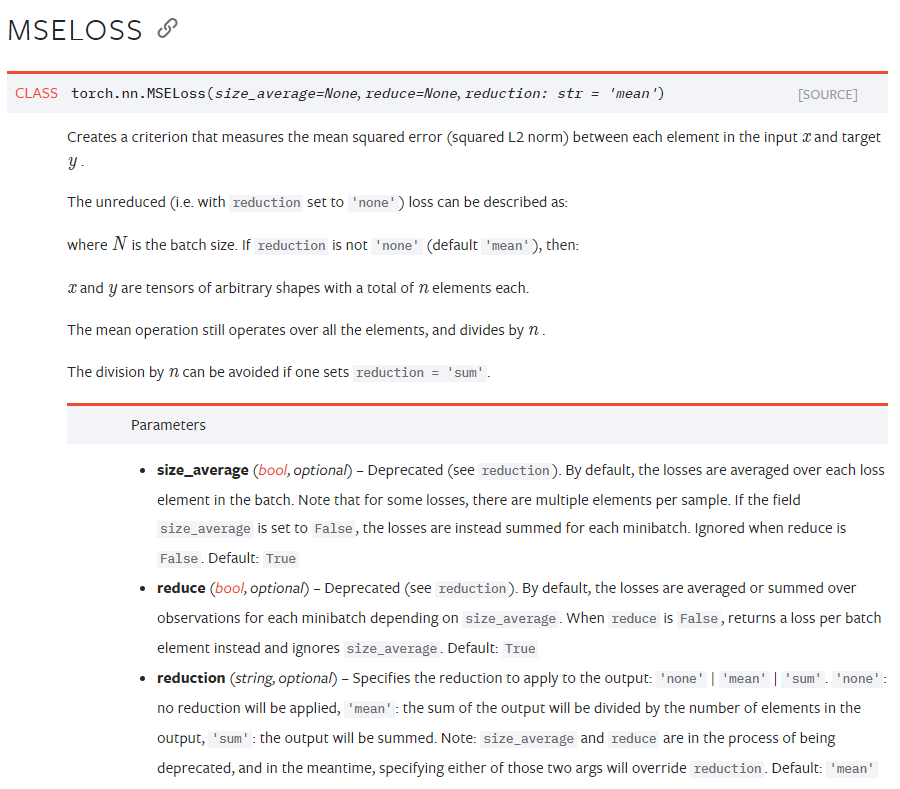
迭代优化器如下所示：

# 不继承于moudle，不会构建计算图
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

通过model.parameters()，提取模型中所有需要更新的参数

接下来写训练过程

for epoch in range(100):
	y_pred = model(x_data)
	loss = criterion(y_pred, y_data)
	print(epoch, loss)
	
	optimizer.zero_grad()
	loss.backward()
	optimizer.step() #更新

输出与测试

# Output weight and bias
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())

# Test Model
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)

引用

[1] 河北工业大学刘洪普老师的视频教程